P1003

信息

此题目来自洛谷，原始题目与提交代码请前往 P1003 [NOIP 2011 提高组] 铺地毯 - 洛谷。

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 $n$ 张地毯，编号从 $1$ 到 $n$ 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 $n+2$ 行。

第一行，一个整数 $n$ ，表示总共有 $n$ 张地毯。

接下来的 $n$ 行中，第 $i+1$ 行表示编号 $i$ 的地毯的信息，包含四个整数 $a,b,g,k$ ，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 $(a,b)$ 以及地毯在 $x$ 轴和 $y$ 轴方向的长度。

第 $n+2$ 行包含两个整数 $x$ 和 $y$ ，表示所求的地面的点的坐标 $(x,y)$ 。

输出格式

输出共 $1$ 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

输入输出样例

输入 #1

输出 #1

输入 #2

输出 #2

-1

说明/提示

【样例解释 1】

如下图， $1$ 号地毯用实线表示， $2$ 号地毯用虚线表示， $3$ 号用双实线表示，覆盖点 $(2,2)$ 的最上面一张地毯是 $3$ 号地毯。

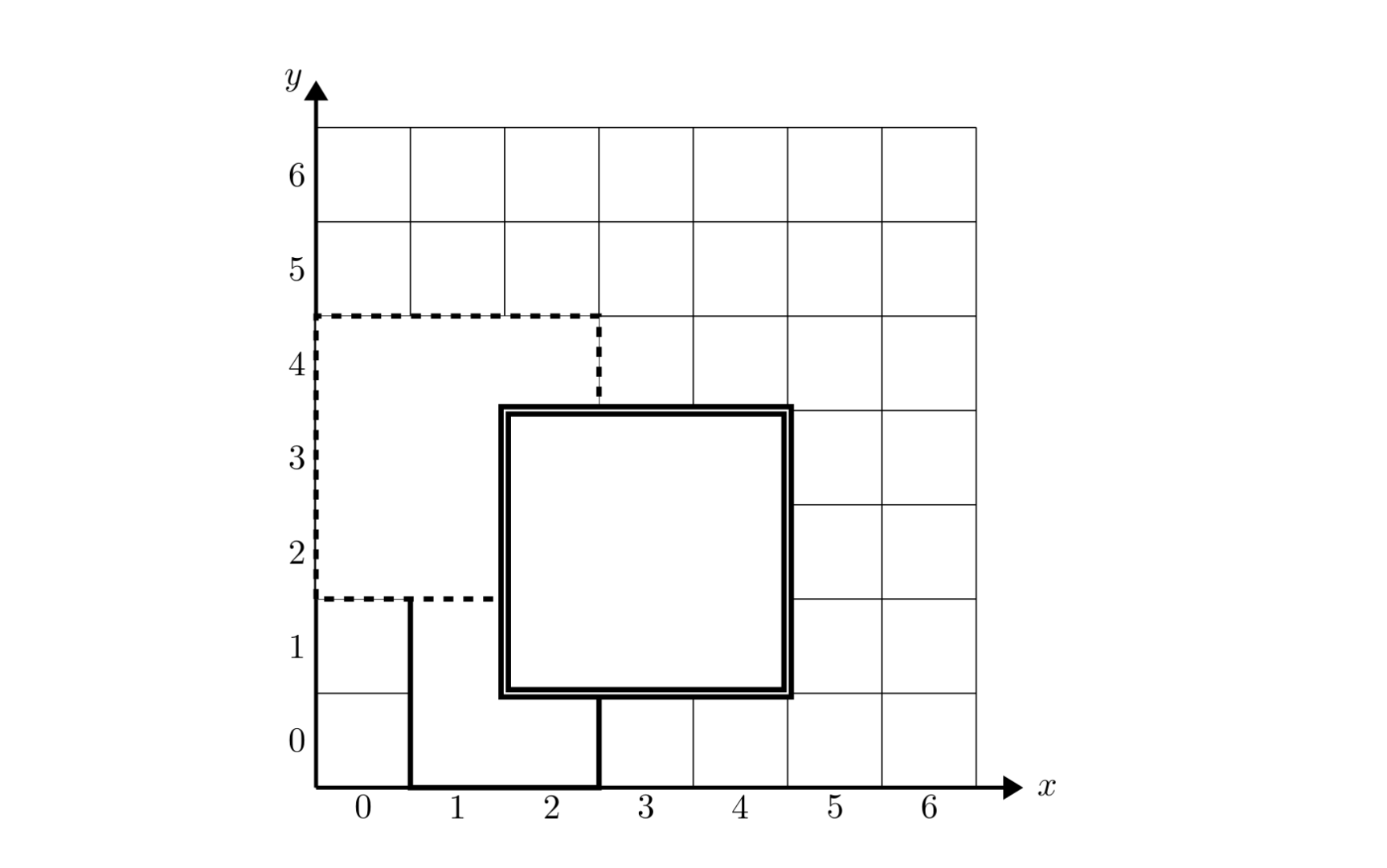
【数据范围】

对于 $30\%$ 的数据，有 ${n}\le{2}$ 。

对于 $50\%$ 的数据， ${0}\le{a,b,g,k}\le{100}$ 。

对于 $100\%$ 的数据，有 ${0}\le{n}\le{{10}^{4}},{0}\le{a,b,g,k}\le{{10}^{5}}$ 。

noip2011 提高组 day1 第 1 题。

题目解答

显而易见，我们直接用一个类记录地毯的数据即可。我实现了一个方法来确认某点是否在地毯中。

之后，我们从后往前遍历，因为题目要求的是最上面的地毯。

/**
 * 洛谷 P1003 解答程序。
 * @author CoolCLK
 */
#include <iostream>
#include <vector>
#define repeat(n) for (size_t _ = 0; _ < n; _++)
using namespace std;

void acceptInput() {}

/**
 * 接受多个参数的输入。
 * @author CoolCLK
 */
template <typename T, typename... Args>
void acceptInput(T& first, Args&... args) {
    std::cin >> first;
    acceptInput(args...);
}

/**
 * 确认值在范围内。
 * @author CoolCLK
 */
template <typename T>
bool isInRange(T num, T a, T b) {
    return num >= min(a, b) && num <= max(a, b);
}

/**
 * 长方形。
 * @author CoolCLK
 */
class Rectangle {
public:
    pair<int, int> position;
    pair<int, int> size;

    Rectangle(int x, int y, int w, int h) {
        this -> position = pair(x, y);
        this -> size = pair(w, h);
    }

    /**
     * 判断是否在范围内。
     * @author CoolCLK
     */
    bool isInBoundingBox(pair<int, int> other) {
        int x = this -> position.first, y = this -> position.second, w = this -> size.first, h = this -> size.second, oX = other.first, oY = other.second;
        return isInRange(oX, x, x + w) && isInRange(oY, y, y + h);
    }
};

int main() {
    int n;
    acceptInput(n);
    vector<Rectangle*> carpets(0, nullptr);
    repeat(n) {
        int a, b, g, k;
        acceptInput(a, b, g, k);
        carpets.emplace_back(new Rectangle(a, b, g, k));
    }
    int x, y;
    cin >> x;
    cin >> y;
    for (int i = carpets.size() - 1; i >= 0; i--) { // 优先取最上面的，因而从后往前遍历
        Rectangle* carpet = carpets[i];
        if (carpet -> isInBoundingBox(pair(x, y))) {
            cout << i + 1 << endl;
            return 0;
        }
    }
    cout << -1 << endl;
    return 0;
}

题目描述​

输入格式​

输出格式​

输入输出样例​

说明/提示​

题目解答​