过河卒

信息

此题目来自 洛谷， 原始题目与提交代码请前往 P1002 [NOIP 2002 普及组] 过河卒 - 洛谷。

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

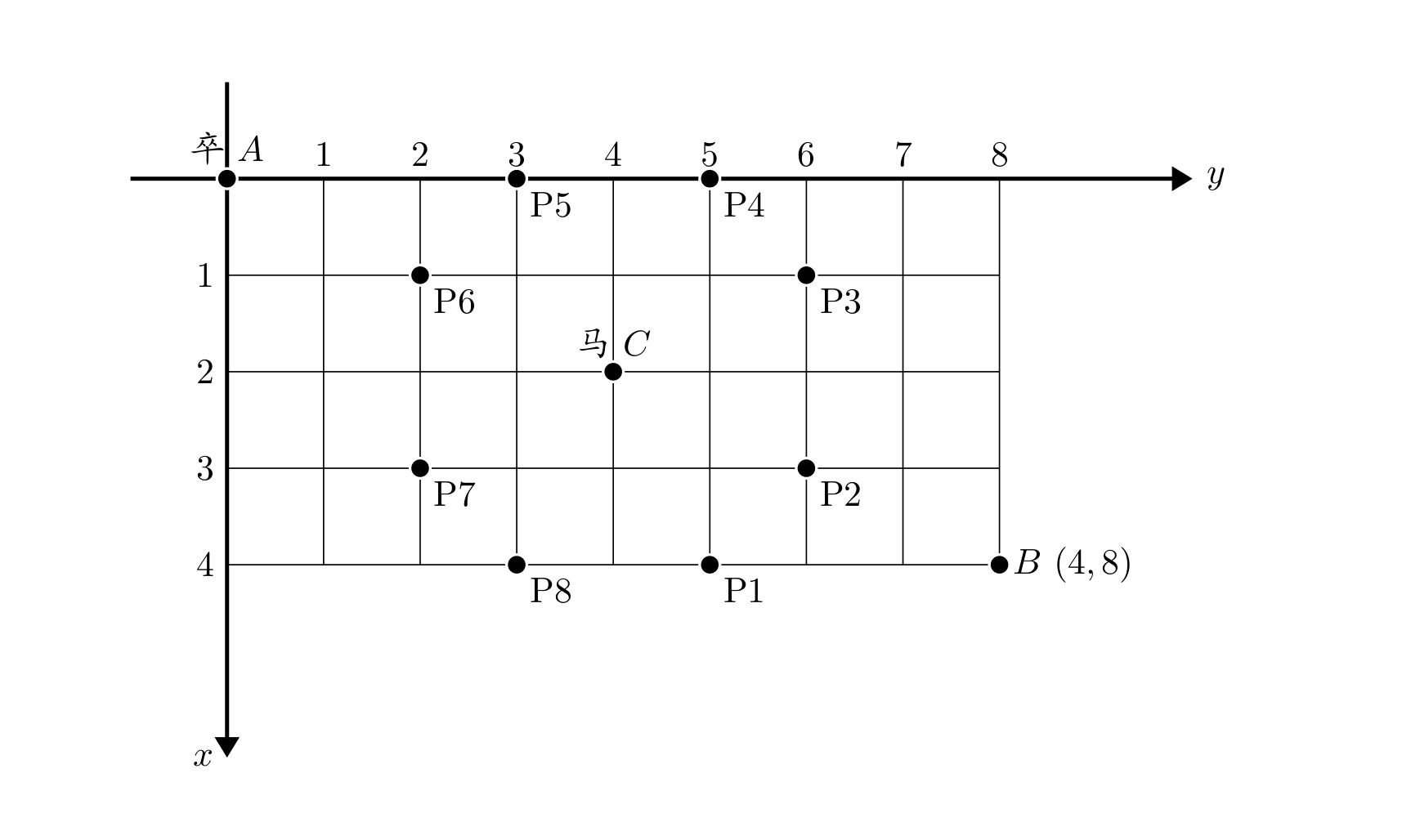
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1

6 6 3 3

输出 #1

6

说明/提示

对于 $100\%$ 的数据，${1}\le{n}$,${m}\le{20}$，${0}\le\text{马的坐标}\le{20}$。

【题目来源】

NOIP 2002 普及组第四题

题目解答

显而易见，像这类求路径数量的题目都涉及到了 动态规划。 那么我们可以从题目得到 $B(n,m), 马(p,q)$，设 $卒(i, j)$。

由于卒到达下一个点要么是从左边移动了 1 步过来的， 要么是从上面移动了 1 步过来的， 可以得到一个状态转移方程 $dp[i][j] = dp[i - 1][j] + dp[i][j - 1]$。

再对碰到马的控制点的 dp 跳过即可。

C++

/**
 * 洛谷 P1002 解答程序。
 * @author CoolCLK
 */
#include <iostream>
#include <vector>
typedef long long l_long;
using namespace std;

void acceptInput() {}

/**
 * 接受多个参数的输入。
 * @author CoolCLK
 */
template <typename T, typename... Args>
void acceptInput(T& first, Args&... args) {
    std::cin >> first;
    acceptInput(args...);
}

int main() {
    int m, n, p, q; // B(n,m),马(p,q)
    const int addP[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
    const int addQ[] = {0, 1, 2, 2, 1, -1, -2, -2, -1}; // 马控制点的相对坐标
    
    acceptInput(n, m, p, q);

    vector<vector<l_long>> dp(n + 1, vector<l_long>(m + 1, 0));
    vector<vector<bool>> controlled(n + 1, vector<bool>(m + 1, false));

    for (int i = 0; i < 9; ++i) {
        int ap = p + addP[i];
        int aq = q + addQ[i];
        if (ap >= 0 && ap <= n && aq >= 0 && aq <= m) {
            controlled[ap][aq] = true;
        }
    }

    dp[0][0] = 1; 

    for (int i = 0; i <= n; ++i) {
        for (int j = 0; j <= m; ++j) {
            if (controlled[i][j]) continue;
            // 非原点(0, 0)
            if (i > 0) dp[i][j] += dp[i - 1][j];
            if (j > 0) dp[i][j] += dp[i][j - 1];
        }
    }

    cout << dp[n][m] << endl;

    return 0;
}